megindulásának

  • Tárgyak
  • Összegzés
  • Bevezetés
  • Eredmények
  • A maximális elmozdulás időbeli alakulása
  • Modell illesztés a paraméter becsléséhez
  • Robusztus teszt és elemzés.
  • Vita
  • Mód
  • Adatfeldolgozás és az átlagos csúcstömítés kiszámítása
  • további információ
  • Kiegészítő információk
  • PDF fájlok
  • Kiegészítő információk
  • Hozzászólások

Tárgyak

Összegzés

A földrengés szakadásának magképződését és terjedési folyamatát laboratóriumi kísérletek és elméleti modellek segítségével vizsgálták, de korlátozott számú léptékű megfigyelés létezik a földrengés törési zónáiról. Különböző modelleket javasoltak, és nyitott kérdést jelent, hogy a bontás folyamatában megjósolható-e a nagyságrend. Itt megmutatjuk, hogy a P hullám maximális elmozdulásának időbeli alakulása informatív a kitörési folyamat kezdeti szakaszához képest, és felhasználható a kitörés végső méretének proxyjaként. Az elemzett földrengések halmaza esetében a kezdeti növekedés gyors növekedését tapasztaltuk kis események esetén, és lassabb növekedést a nagy földrengések esetén. Eredményeink azt mutatják, hogy a nagy kritikus csúszástávolságú régióban előforduló földrengések nagyobb valószínűséggel növekednek nagy szakadásra, mint azok, amelyek rövidebb csúszási-fakulási távolságú régióból származnak.

Bevezetés

A szakadás kezdete iránt a közelmúltban ismét felkeltették az érdeklődést, mivel annak a földrengés nagyságának gyors felmérésére gyakorolt ​​közvetlen hatása van. A földrengés korai figyelmeztető rendszerei által kiváltott kockázatcsökkentő intézkedések szempontjából kulcsfontosságú az a képesség, hogy az első P-hullám megfigyelésének elemzésével helyesen meg lehessen különböztetni a kis sokkot a nagy eseménytől. Számos szerző kimutatta, hogy a rögzített P hullámok első része a nagyságrendről tartalmaz információt a 17, 18, 19, 20 frekvencia és/vagy amplitúdó tartalma révén. Ezen tanulmányok többsége egy fix P-hullámú időablak (PTW; 3–4 s) elemzésére összpontosított.

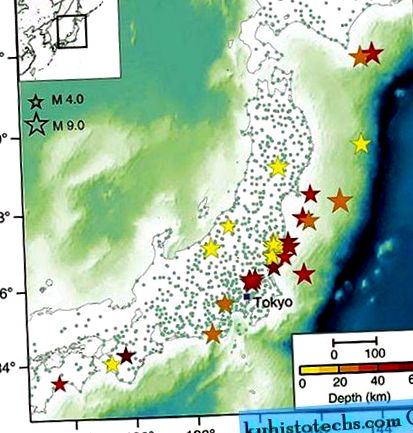
Jelen tanulmányban a szűrt P-hullámú jelek (Pd) maximális elmozdulási amplitúdóját mértük egy fokozatosan bővülő PTW felett. A hullámformák kezdetének korábbi tanulmányai néhány, ugyanahhoz a szekvenciához tartozó, korlátozott számú állomáson vagy földrengésen rögzített földrengéseket elemeztek. Ilyen körülmények között nehéz lehet egyértelműen felismerni és megkülönböztetni a forrás és a terjedési hatásokat, amelyek befolyásolhatják a jelek kezdeti alakját. Itt egy nagyobb, jó minőségű, 43 közepes és erős japán esemény adatait használjuk, amelyek nagy nagyságrendű (M) és távolsági (R) tartományokat ölelnek fel (4≤ M ≤9; 0≤ R ≤500 km). Több mint 7000 háromkomponensű, 1120 állomáson rögzített hullámformát elemeztünk. Az elemzett események teljes listáját az 1. Kiegészítő táblázat tartalmazza, míg az adatbázis-kiválasztással kapcsolatos további részletek a Kiegészítő módszerek részben találhatók. Az 1. ábra az alkalmazott állomások térképét és a kiválasztott események epicentrumait mutatja.

A tanulmányban használt állomások megoszlása ​​(kis zöld körök) és a 43 kiválasztott esemény epicentrális helyszíne (színes csillag). A csillag mérete arányos a nagyságával, a szín pedig a forrás mélységét jelenti. A jobb alsó sarokban található fekete sáv 100 km hosszúságot jelöl.

Teljes méretű kép

Eredmények

A maximális elmozdulás időbeli alakulása

Az elemzett földrengések száma garantálja a megfelelő adatmintavételt nagyságú és távolságú konténerekben (2a. - c. Ábra). Minden eseménynél a P d és PTW görbe logaritmusát (a továbbiakban rövidítve: LPW görbe) úgy kapjuk meg, hogy az összes rendelkezésre álló állomás adatait átlagoljuk egyszerre (általában több mint 100; lásd: Módszerek szakasz). Megállapítottuk, hogy minden görbe az idő múlásával fokozatosan növekszik, amíg el nem érjük a végleges értéket. A fennsík szintje (PL) és a telítettségi idő általában nagyságrendileg növekszik (3a. Ábra).

( nak nek ) A földrengések számának hisztogramja a nagyságrend függvényében. ( b ) A nagyság megoszlása ​​a kiválasztott események mélységének függvényében. ( c ) A rekordok eloszlása ​​a távolság függvényében különböző nagyságrendű osztályokhoz.

Teljes méretű kép

( nak nek ) A P d görbe átlagos logaritmusa a PTW (LPW) függvényében minden elemzett esemény esetében. Az y tengely a P d átlagos logaritmusát jelenti, amelyet az egyes időpontokban rendelkezésre álló összes adat felhasználásával kaptunk, miután az egyes értékeket korrigáltuk a távolság hatására (az 1. egyenlet felhasználásával). A beszúró doboz a darabonkénti lineáris illesztés függvény vázlatos ábrázolása. ( b, c, d ), Példa három M 4.7 nagyságú reprezentatív esemény LPW görbéjére ( b ), 6,7 ( c ) és 9 ( d ), ill. Minden panelen a szürke körök a megfigyelt adatok, a hozzájuk tartozó hibasávokkal ± 1σ (szaggatott vonalak). A folytonos vonal a legjobban illeszkedő függvény, amelyet darabonkénti lineáris modell alkalmazásával kapunk, és a sötét négyzetek minden esemény T1 és T2 idejét jelölik.

Teljes méretű kép

Egyetlen állomás esetében a távoli mező kinematikai modelljei azt mutatják, hogy a P d/idő görbe megismétli a látszólagos 21 forrás idő alakját. Azáltal, hogy P d-t átlagolunk sok állomás között, elosztva azimutban és távolságban, a kapott függvény közelíti az MRF-et. Ha feltételezzük, hogy az MRF háromszög alakú, akkor a P d és az idő görbék fennsíkját az MRF csúcsán érjük el, és a megfelelő idő a forrás pillanat és időtartam proxyja 22. Megfigyeléseink azt mutatják, hogy a P d és az idő görbék kezdeti alakja általában exponenciális trendet követ.

Modell illesztés a paraméter becsléséhez

Bár ezek a becslések a teljes lebontási folyamatra vonatkoznak, a kezdeti csökkenés valószínűleg nem eredményez végleges állandó értéket, függetlenül a nagyságától. Ezzel szemben, feltételezve, hogy D c esetén egy M = 7 27 esemény 0,5–1 m jellegzetes értéke, az M = 4,5 esemény megfelelő értéke az 5–10 cm skálán lenne. Ezt az értéket negatív nagyságrendekre extrapolálva, a laboratóriumi kísérletek becslései szerint Dc esetén mikrometrikus és milliméteres értékeket kapunk. Egy ilyen skála azt jelzi, hogy nagyobb törési energia áll rendelkezésre a szakadás kezdeti szakaszában nagyobb események esetén. Ezenkívül a magképződés nagysága közvetlenül összefügg a 28 csúszás elhalványulásának lineáris modelljein tapasztalható fakulás mértékével, ami a nagyobb események nagyobb méretét és hosszabb jellegzetes nukleációs idejét sugallja, amit a T1 pozitív nagyságrendű pozitív skálája is megerősít.

A nagyságrendileg növekvő szakadási energiát a földrengéses törésmechanikában általában a töréssíkban lévő összes versenyképes disszipatív mechanizmus homogenizált hatásaként értelmezik, mint például a súrlódás, a hibán kívüli károk, a hőnyomás és az egyesülés 29. Kiterjesztve ezt az értelmezést a szakadás kezdeti szakaszára, a hiba mentén bekövetkező lehetséges D c változások összefüggésben lehetnek a 3 érdességek jellegzetes hosszával vagy a hiba zóna belső merevségével, amely a hiba során rugalmasan felhalmozza az energiát. Betöltés. Feltételezve, hogy a hibában a változó D c fraktáleloszlás némi térbeli koherenciával áll, azt állítjuk, hogy amikor egy alacsony D c értékű régióban szeizmikus szakadás alakul ki, akkor a szomszédos régiókban való repedés valószínűsége alacsony. Ezzel ellentétben, ha egy koherens törés egy nagyobb Dc régióban kerül kialakításra, akkor valószínűbb, hogy nagyobb eseménysé válik. Ebben az összefüggésben a D c és a kezdeti szeizmikus repedés növekedésének valószínűségének változása igazolja a B1 értékek diszperzióját a nagyságrendhez képest.

Végül az MRF és a B1 közötti log-lineáris összefüggés a nukleációs fázis exponenciális növekedését jelzi. Bár a megfigyelt T1 értékek összehasonlíthatók a magképződési időkkel, nem zárhatjuk ki annak lehetőségét, hogy ezek a dinamikus lebontási fázis kezdeti gyorsulását jelentik. Ezenkívül a magasabb bomlási energia megakadályozza a bontás gyors felgyorsulását ebben a korai szakaszban, ami szintén korlátozza a pillanatnyi sebesség növekedését.

A B1 megfigyelt nagyságrendű változása nagy hatással lehet a földrengés méretének gyors felmérésére. Azonban az ebben a munkában mért meredekség a rekordok százainak átlagos tendenciájából származik, széles azimut- és távolságtartományokat felölelve, míg valós időben az adatok rendelkezésre állása az origóállomás geometriájától függ. Ezért további elemzésre van szükség az adatok valós idejű továbbításának szimulálásához és a kezdeti meredekség korlátozásához szükséges minimális, közel eredetű adatok értékeléséhez. Feltételezve, hogy a lejtés jól korlátozott a forráshoz közeli adatokból, egy rövid időablak (kb. 1 s, Kiegészítő 7. ábra) elegendő a földrengés nagyságának értékeléséhez.

Mód

Adatfeldolgozás és az átlagos csúcstömítés kiszámítása

Az elmozdulás hullámformáinak megszerzéséhez az átlagértéket és a lineáris trendet először eltávolítják a nyers gyorsulási adatokból. Ezeket a rekordokat kétszeresen integrálják, és 0,075 Hz-es vágási frekvenciájú, nem okozati szempontból magas áteresztésű Butterworth-szűrőt alkalmaznak a kettős integrációs művelet által bevezetett hosszú távú mesterséges trend és az alapvonalak kiküszöbölésére. A P hullám kezdési idejét manuálisan választottuk ki a gyorsulásmérő felvételeinek minden vertikális komponenséből.

Mérjük a maximális elmozdulási amplitúdót a szűrt P-hullám jelekben (Pd) egy fokozatosan bővülő PTW-n keresztül, a P hullám kezdési időpontja utáni 0,05 s-tól kezdve és folytatva az S-fázis 30 várható megérkezéséig. Minden eseményhez úgy kaptuk meg az LPW görbét, hogy átlagoltuk az összes rendelkezésre álló adatot az egyes időablakokban, miután kijavítottuk a különböző állomásokon megfigyelt Pd értékeket a geometriai csillapítás hatására. A különböző állomásokon megfigyelt Pd értékek összehasonlításához a geometriai csillapítási hatást a következő csillapítási összefüggéssel korrigáltuk:

ahol M az esemény nagysága, P d-t cm-ben (rögzített 3 másodperces időablakban) és az R hipocentrális távolságot km-ben mérjük. Az (1) egyenletben egyetlen kifejezést (log R) használnak mind a geometriai szórás, mind az anelasztikus csillapítás magyarázatára. Az itt használt mennyiségeket a Japán Meteorológiai Ügynökség biztosítja, és feltételezhetően ekvivalensek a jelenlegi mennyiségekkel. Az M-lel történt földrengésekhez

ahol T p a megfigyelt P hullám kezdési ideje, R a hipocentrális távolság km-ben és b = 0,088. A b együtthatót lineáris regresszióanalízissel kaptuk meg, miután manuálisan kiválasztottuk az S hullám érkezési idejét korlátozott számú rekord számára az adathalmazunkban.

Minden eseményhez meghatározunk egy maximális felfedezhető PTW-t, a kinematikai modellek forrásának várható időtartama alapján, a megfelelő nagyságrend alapján, és legalább a várható időtartam kétszeresét vesszük figyelembe. Az átlagos LPW görbe kiszámításához legalább öt adatpontot is megkövetelünk minden egyes PTW-hez. Az átlagos számítás leáll, ha az adatpontok száma nem elegendő, vagy ha a PTW eléri a maximális határidőt, attól függően, hogy melyik feltétel következik be először.

Az LPW görbék modellezéséhez fordított, darabonkénti lineáris illesztési függvényt használunk öt ismeretlen paraméterhez: az első és a második sarokidőhöz (T1 és T2, ill.), A két egyenes meredekségéhez (B1 és B2, illetve a Final) PL.

további információ

Hogyan idézhetem ezt a cikket: Colombelli, S. és mtsai. Bizonyíték a szakadás kezdetének különbségére a kis és nagy földrengések között. Nat. Commun. 5: 3958 doi: 10.1038/ncomms4958 (2014).

Kiegészítő információk

PDF fájlok

Kiegészítő információk

1-7. Kiegészítő ábra, 1-2. Kiegészítő táblázat, kiegészítő vita, kiegészítő módszerek és kiegészítő hivatkozások

Hozzászólások

Megjegyzés beküldésével vállalja, hogy betartja a közösségi feltételeket és irányelveket. Ha valami visszaélést tapasztal, vagy nem felel meg feltételeinknek vagy irányelveinknek, kérjük, jelölje meg nem megfelelőnek.