Bevezetés

Ez az öntanulási modul: "Operációkutatás: LINEÁRIS PROGRAMOZÁS" Ezt az Operációkutatás Szakmai Energetikai Mérnökiskola hallgatói számára fejlesztették ki, hogy segítsék őket ennek a tág tudományágnak az elsajátításában és néhány pedagógiai igény kielégítésében.

A modult a könyvek létező különféle módszertanainak figyelembevételével és a hallgatók pedagógiai igényeihez igazítva fejlesztették ki, és öt tanulóra osztották, figyelembe véve az egyes témákhoz kapcsolódó néhány rövidített tevékenységet, ahol a hallgatónak ellenőriznie kell tanulás és az egyes foglalkozások végén önértékelésnek minősül. A hallgatók nem léphetnek tovább a következő foglalkozásra, ha nem fejezték be az összes tervezett tevékenységet.

A foglalkozások tartalma a következő:

01. foglalkozás: A műveletek kutatásának alapjai, irányítja a hallgatókat az operációkutatás módszertanának összefüggésében a főbb meghatározások, alkalmazási területeik és a kidolgozott operációkutatási technikák megadásával.

02. foglalkozás: A lineáris programozás alapjai, bemutatja a lineáris programozási technika ismeretét, felépíti annak modelljeit és egyes elemeinek leírását; A modellek problémás helyzetekből vannak megfogalmazva, grafikus módszerrel megoldva őket. Emellett tanulmányozzák a hozzárendelés, a szállítás és az étrend problémáját.

03. ülés: Simplex Primal módszer, A hallgatók megtanulják megoldani a lineáris programozási modelleket az elsődleges szimplex algoritmus segítségével, adminisztratív értelmezést adva az eredményeknek, és egyfajta megoldást rendelve hozzá.

04. ülés: A kettős probléma és a szimplex kettős módszer, A hallgató a kettős problémát az elsődleges problémából fogja felépíteni, a kettős eredményeit pedig a Primal megoldásából adja meg. Ezenkívül megtanulja a Simplex Dual algoritmust, mint PL hibaelhárítási alternatívát, amely megfelel ennek a technikának a feltételeivel.

05. foglalkozás: Érzékenység elemzése, A hallgató képes lesz értelmezni a lineáris programozási technika eredményeit, értékelve erőforrásainak és/vagy nyereségének (költségeinek) növelésének vagy csökkentésének lehetőségeit, tiszteletben tartva a megvalósíthatóság és az optimalitás feltételeit.

Ezzel az önálló tanulmányi modullal hozzájárulni kívánok a mérnöki hallgatók számára az operációkutatás pedagógiai területén, és nyitott vagyok minden javaslatra vagy építő kritikára a továbbfejlesztés érdekében, és ez az oka annak, hogy minden szakembernek lenni.

Operációkutatás

1. A MŰVELETEK VIZSGÁLATÁNAK MEGHATÁROZÁSAI.

"Az I. O. tudományos döntéshozatali megközelítésként írható le, amely megköveteli a szervezeti rendszerek működését".

Hiller és Lieberman

"Az I. O. megérti az alkalmazott matematika módszereit és modelljeit a komplex műveletek problémáinak megoldására".

Az elnöki bizottság a Biztonság területén

Észak-Amerika USA Repülés.

"Az I. O. tudományos módszerek, technikák és eszközök alkalmazása olyan problémákra, amelyek magukban foglalják a rendszerek működését, valamint optimális megoldásokat kínálnak számukra a működésük ellenőrzésének problémáira".

Churchman, Ackoff és Arnoff

"Az I. O. magában foglalja a tudományos módszer alkalmazását nagy és összetett szervezetek vagy tevékenységek tanulmányozására"

Nagy-Britannia Nemzeti Kutatási Tanácsa

"Az I.O. meghatározása a tudományos módszer alkalmazása a vezetői döntési problémák elemzésére és megoldására"

Turban és Meredith

"Az I.O. kifejezést itt a matematikai modellek felhasználásának elemzéseként használják a döntéshozatali segédletként"

Buffa és Dyer

A Dominikai Köztársaság Santiagói Műszaki Egyetem Operációirányítási Mesterének Operatív Kutatási Technikák tanfolyamának tananyagából származik.

MŰVELETEK VIZSGÁLATI TANULMÁNY MŰKÖDÉSI SORBA.

műveletek kutatásának

A Dominikai Köztársaság Santiagói Műszaki Egyetem Operációirányítási Mesterének Operatív Kutatási Technikák tanfolyamának tananyagából származik.

2. A MŰVELETEK VIZSGÁLATÁNAK TERÜLETEI.

Az operációs kutatás olyan témákkal foglalkozik, amelyek a következő kérdésekre adnak választ:

Hogyan lehet a leghatékonyabban elosztani bizonyos szűkös erőforrásokat a legmagasabb megtérülési arány elérése érdekében? Mi lehet a legjobb módja annak, hogy olyan útvonalakat hozzárendeljen egy olyan termékflottához, amelyet a forgalmazók raktáraiban kell elhelyezni, hogy az alacsonyabb legyen? Hány ablakot kell elhelyezni egy bankban normál órákban, csúcsidőben és napokon, hogy az ügyfelek ne essenek kétségbe és vonuljanak ki az utca túloldalán lévő bankba (verseny)?

Amint láthatja, az üzemeltetési kutatás területe változatos: alkalmazható bármely emberi tevékenységben, de elsősorban az adminisztrációban, a gazdaságban, az iparban és a mérnöki tevékenységben, mindig az erőforrások optimalizálására törekedve.

3. MŰVELETEK VIZSGÁLATI TECHNIKA.

A műveletek kivizsgálásának leggyakrabban alkalmazott technikái közül megemlíthetjük a következőket:

Lineáris és egész programozás: Ez a problémák matematikai modellek szerinti megfogalmazásából áll, amelyek célja az előnyök vagy költségek maximalizálása vagy minimalizálása. A lineáris programozás az egész programozástól némileg eltér a technika tekintetében, hogy az eredményeket megtalálja az általa felvett értékek alapján.

Dinamikus programozás.- A dinamikus programozást lineáris és nemlineáris problémák esetén egyaránt alkalmazzák. Hasznos egy olyan probléma megoldásában, ahol egymással összefüggő döntések sorozatát kell meghozni. A lineáris programozástól eltérően a dinamikus programozásnak nincs standard matematikai megfogalmazása. Ez egy általános megközelítés a problémák megoldására, és az egyenletek a problémák egyedi körülményeiből származnak.

Projektek programozása és értékelése PERT - CPM - mel.: A projekttervezésnek ez a technikája par excellence vezetői eszköz, mivel lehetővé teszi az ügyvezető számára, hogy végrehajtásuk során nagyon pontos ellenőrzést tervezzen és tartson fenn.

Készletelmélet.- Leltár akkor jön létre, amikor a kapott anyagok, alkatrészek vagy késztermékek mennyisége nagyobb, mint az elosztott mennyisége; a készlet kimerül, ha az elosztás nagyobb, mint az anyagok beérkezése. A készletelmélet a különféle készletgazdálkodási modellek tanulmányozását szolgálja oly módon, hogy lehetővé tegye számunkra a szükséges rendelkezésre álló erőforrások fenntartását anélkül, hogy költségeik lennének, ha hiányuk vagy többletük van. Számos olyan módszer közül, amelyek lehetővé teszik számunkra az optimális leltárt, ezek között van: ABC osztályozás, JUST IN TIME (JIT) modell, Anyagigény-tervezési modell (MRP), EOQ-modell determinisztikus igényekkel stb.

Döntéselmélet.- mindannyian mindig különböző belső vagy külső tényezők által befolyásolt döntéseket hozunk, amelyek eredménye kedvező vagy kedvezőtlen lehet. Egyes esetekben a döntések eredménye kiszámítható, más esetekben azonban nagy a bizonytalanság. A döntéselmélet a döntéshozatal tanulmányán alapul, felhasználva a korábbi információk alapján a valószínűségeket, oly módon, hogy korábban kiszámolják a döntés megütésének esélyét. Néhány technika: BAYES elmélet, MINIMUM, MAXIMIN, MAXIMUM kritérium stb.

A farok elmélete.- A várólisták gyakori szó az életünkben, például ha pénzt akarunk szerezni egy ATM-től, amikor kórházba megyünk, meghibásodott gépeket várunk javításra stb., Mindez következményként kényelmetlenséget és költségeket okoz. tény, hogy a sorok. Ez az elmélet bizonyos technikák kifejlesztésén alapul a kényelmetlenség csökkentése, a rendszer hatékonyabbá tétele és ezáltal a költségek csökkentése érdekében.

Játékelmélet.- körkörös érvelésből áll, amelyet a stratégiai kérdések mérlegelésekor nem lehet elkerülni. Az ember természeténél fogva nem jár jól a stratégiai kapcsolati problémákra gondolva, mivel a megoldás általában fordított logika.

A játékelméletben az intuíció nem túl megbízható stratégiai helyzetekben, ezért oktató példák figyelembevételével kell képezni, anélkül, hogy valódinak kellene lenniük.

A Game Theory-nak jelenleg sok alkalmazása van, azonban a Game Theory szakemberei által készített ötletek számára a közgazdaságtan a fő vásárló. Azon tudományterületek között, ahol a játékelmélet alkalmazható, van: közgazdaságtan, államtudomány, biológia és filozófia.

4. A MŰVELETEK VIZSGÁLATÁNAK MINTÁI.

A modell a valóságnak az elemzés termékeként való ábrázolása a vizsgálata céljából.

Modellek típusai:

Ikonikus modell: Konkrét, valóságos tárgy ábrázolása (fotó, modell).

Szimbolikus modell: Keresleti görbe a közgazdaságtanban.

Matematikai modell: Az ezen a ponton szereplő egyenleteket feltételezzük, hogy a modell a problémás helyzet tényleges ábrázolása.

Ezt a modellt használják az operációkutatások.

ÖNÉRTÉKELÉS

1) Írjon egy Operációkutatási koncepciót.

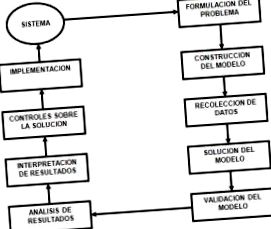
2) Példa segítségével magyarázza el az operációkutatás lépéseinek sorrendjét!.

3) Készítsen összefoglaló táblázatot a műveletek kivizsgálásának technikáiról.

4) Magyarázza el a 3. példa műveletkutatási technikáit!.

5) Írjon modellkoncepciót és adjon példákat a modelltípusokra!.

CSAPAT MUNKA: Alakítson 5 fős csoportokat, és kutassa a következő témákat:

A műveletek kutatásának történelmi háttere.

Vizsgálja meg, hogy a speciális műveletek kutatásának mely területein alkalmazták.

Készítsen csoportos jelentést és diákat a következő osztály bemutatására.

TÖRTÉNELMI HÁTTÉR.

A második világháború kampányaiban elért sikerek miatt az 1950-es években az iparban, az üzleti életben és a kormányzatban használják.

Olyan karriert eredményezett, mint a gépészeti, vegyipari és ipari mérnöki szak.

Anglia hozta létre ezt a tudományágat, és az Egyesült Államoknak köszönhető a gyors növekedés az 1947-ben George Dantzing. Az IoT egyéb eszközei a PL, P. Dynamics, Waiting Lines és a készletelméletek még az 1950-es évek vége előtt.

A LINEÁRIS PROGRAMOZÁS MEGHATÁROZÁSA.

Ez egy matematikai elemzési technika, amely lehetővé teszi annak megállapítását, hogy melyik a leghatékonyabb elosztása a korlátozott erőforrásoknak a vállalat által végzett tevékenységekben a szervezet célkitűzéseinek optimalizálása, vagyis az előnyök maximalizálása vagy a költségek minimalizálása érdekében.

A LINEÁRIS PROGRAMOZÁSI MODELL ELEMEI.

DÖNTÉSI VÁLTOZÓK:

A modell ismeretlen (X1, X2, X3,., Xn)

PARAMÉTEREK: A rendszer vezérelhető változói. (aij)

CÉL FUNKCIÓ: maximalizálás vagy minimalizálás. (Max Zo. Ó Min Zo.)

KORLÁTOZÁSOK: Szűkítő egyenletekként kifejezve a rendszer határforrásait képviselik.

KEDVEZHETŐ RÉGIÓ. Ezek azok a Xi értékek, amelyek igazolják a korlátozásokat. Az adott régió bármely pontja megoldást jelenthet a problémára; bármely pont, amely nem tartozik ebbe a halmazba, nem lehet megoldás.

A probléma optimális megoldása a megvalósítható halmaz értékpárja (Xa, Xb) lesz, amely f (Xa, Xb) értékét a maximális vagy a legkisebb értékre készteti.

VONALOS PROGRAMOZÁSI MODELL

A STANDARD PL SHAPE TULAJDONSÁGAI

Minden kényszer egyenlet (nem negatív második tagokkal, ha a modellt az elsődleges szimplex módszerrel oldják meg.

Minden változó nem negatív.

A célfüggvény lehet maximalizálás vagy minimalizálás.

VÁLTOZÓK TÍPUSAI PL-MODELLBEN

Ha a megkötés formájú (akkor egy BIZTONSÁGI VÁLTOZHATÓ hozzáadódik az If

Ha a megkötés formájú (akkor hozzáadódik egy TÚL VÁLTOZÓ - Ha

Mesterséges változók (Ai): Lazán változóként működik a = formában

Nem alapváltozók: Azok a változók, amelyek értéke nulla.

Alapváltozók: Olyanok, amelyek értéke eltér a nullától. Ha pozitívak, akkor azt mondják, hogy alapvető megvalósítható változók.

Korlátlan (vagy nem korlátozott) változó: yi két nem negatív változóban ábrázolható a következő helyettesítéssel:

A LINEÁRIS PROGRAMOZÁSI MODELLEK KÉPZÉSE ÉS MEGOLDÁSA.

A MAXIMÁLÁSI MODELL KÉSZÍTÉSE.

01. probléma

Két típusú házat kell felépíteni egy urbanizációban: A és B. Az építőipari vállalat erre legfeljebb 1800 millió pesétával rendelkezik, az egyes házak költsége 30, illetve 20 millió. A városi tanács előírja, hogy a házak száma ne haladja meg a 80-at. Annak tudatában, hogy az A típusú ház eladásából származó nyereség 4 millió, a B típusú ház esetében pedig 3 millió, akkor hány típusú házat kell felépíteni megkapja a maximális hasznot?